selfbas.blogg.se - Can you calculate weighted standard deviation continuous

What cumsum() does is that returns a vector whose elements are the cumulative sums of the elements of the arguments. However, in some cases, the function cumsum() may come in handy. We could sum individual probabilities in order to get a cumulative probability of a given value. Let’s go back to our probability density function of the first exercise:Īll the probabilities in the table are included in the dataframe probability_distribution which contains the variables outcome and probs. In this exercise we will jump into cumulative probability distributions. In the last two exercises, we saw the probability distributions of a discrete and a continuous variable.

The cumulative probability distribution cumsum().

# simulating data set.seed ( 11225 ) data <- rnorm ( 10000 ) # check for documentation of the dnorm function help ( dnorm ) # calculate the density of data and store it in the variable density density <- dnorm ( data ) # make a plot with as x variable data and as y variable density plot ( x = data, y = density )

Finally make a plot with as x variable the data vector and as y variable the density variable.

Now calculate the density of the data vector and store it in a vector called density.

Check the documentation of the the dnorm function using help(dnorm).

You will then need to visualize the data. This data is contained within the data vector. In this exercise, we will simulate some random normally distributed data using the rnorm() function. Probabilities here are thus considered surface areas. To get a probability, you will need to consider an interval under the curve of the probability density function. Only the first elements of the logical arguments are used.įor sd = 0 this gives the limit as sd decreases to 0, a point mass at mu. The numerical arguments other than n are recycled to the length of the result. The length of the result is determined by n for rnorm, and is the maximum of the lengths of the numerical arguments for the other functions. The normal distribution has density \(f(x) = \frac\) where (\mu) is the mean of the distribution and (\sigma) the standard deviation.ĭnorm gives the density, pnorm gives the distribution function, qnorm gives the quantile function, and rnorm generates random deviates. If mean or sd are not specified they assume the default values of 0 and 1, respectively.

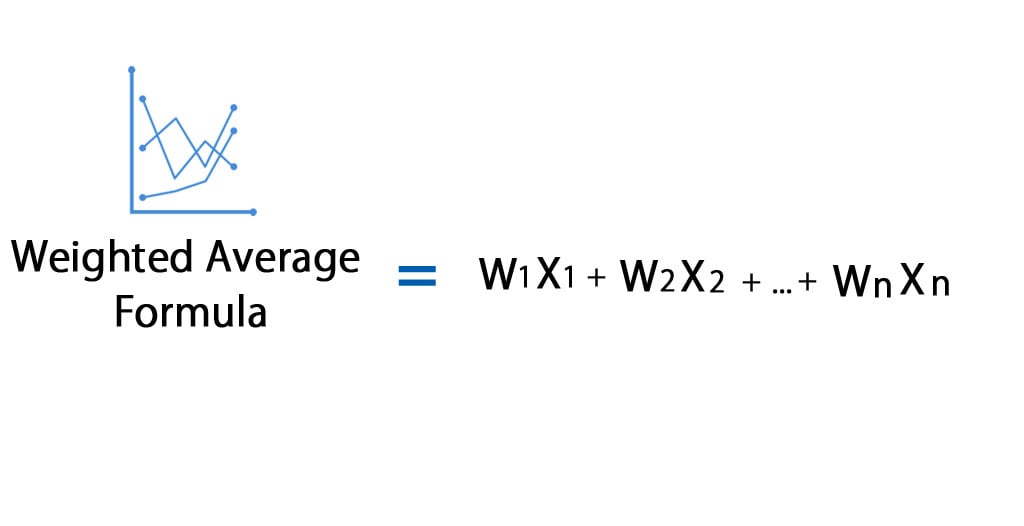
Logical if TRUE (default), probabilities are (P) otherwise, (P). Logical if TRUE, probabilities p are given as log(p). If length(n) > 1, the length is taken to be the number required. Qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) But these extreme distributions arise rather infrequently across a broad range of practical applications.Pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) So clearly, the rule does not apply in some situations. This result is correct (to two decimal places) for an important distribution that we meet in another module, the Normal distribution, but it is found to be a useful indication for many other distributions too, including ones that are not symmetric.ĭue to Chebyshev's theorem, not covered in detail here, we know that the probability \(\Pr(\mu_X - 2\sigma_X \leq X \leq \mu_X + 2\sigma_X)\) can be as small as 0.75 (but no smaller) and it can be as large as 1. This guide or 'rule of thumb' says that, for many distributions, the probability that an observation is within two standard deviations of the mean is approximately 0.95. (The variance is equivalent to the 'moment of inertia' in physics.) However, there is a useful guide for the standard deviation that works most of the time in practice.

the random variable \(V\) from exercise 2.Īs observed in the module Discrete probability distributions, there is no simple, direct interpretation of the variance or the standard deviation.

The mean \(\mu_X\) of a continuous random variable \(X\) with probability density function \(f_X(x)\) is

The equivalent quantity for a continuous random variable, not surprisingly, involves an integral rather than a sum. Where the sum is taken over all values \(x\) for which \(p_X(x) > 0\). In the module Discrete probability distributions, the definition of the mean for a discrete random variable is given as follows: The mean \(\mu_X\) of a discrete random variable \(X\) with probability function \(p_X(x)\) is

When introducing the topic of random variables, we noted that the two types - discrete and continuous - require different approaches. Content Mean and variance of a continuous random variable Mean of a continuous random variable